Neural Networks (NNs) are the heart and soul of today's many active research topics to automate routine tasks, understand all forms of multimedia and make diagnoses. Nowadays, many libraries like PyTorch, TensorFlow, Keras, and Caffe make implementation easy. But many students and users lack the basics of what is going on beneath the function calls of the mentioned libraries.
Here is an example of building a model with PyTorch.
# import modules
import torch
import torch.nn as nn
# define a model with a single fully connected layer
model = nn.Sequential(nn.Linear(n_input, n_hidden),
nn.Linear(n_hidden, n_out),
nn.Tanh())
These few lines of code are capable of predicting what a vector of numbers represents. But do we precisely know, what is going on under the hood? If not, this series will deepen your understanding as we build a model with simple python.
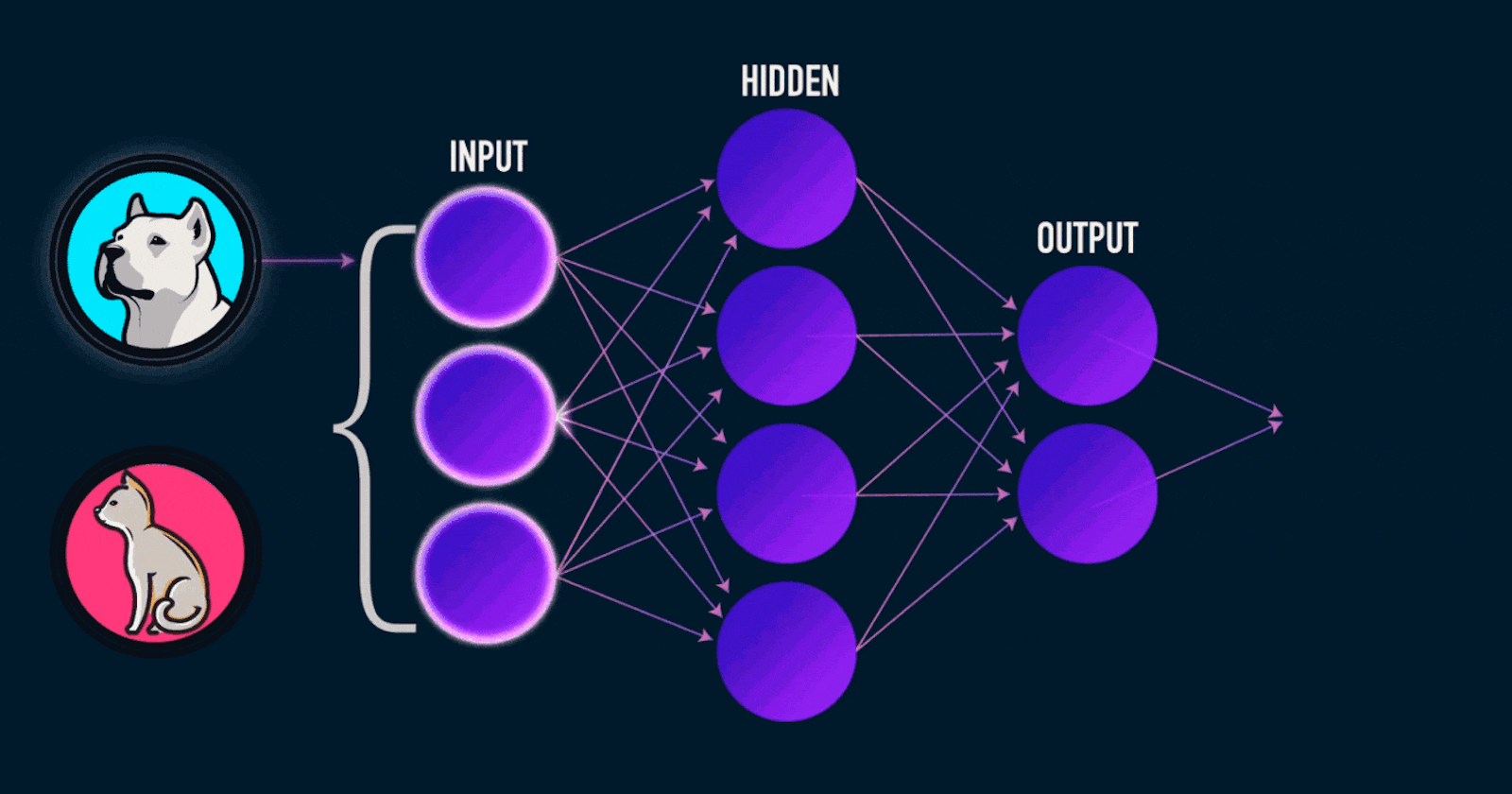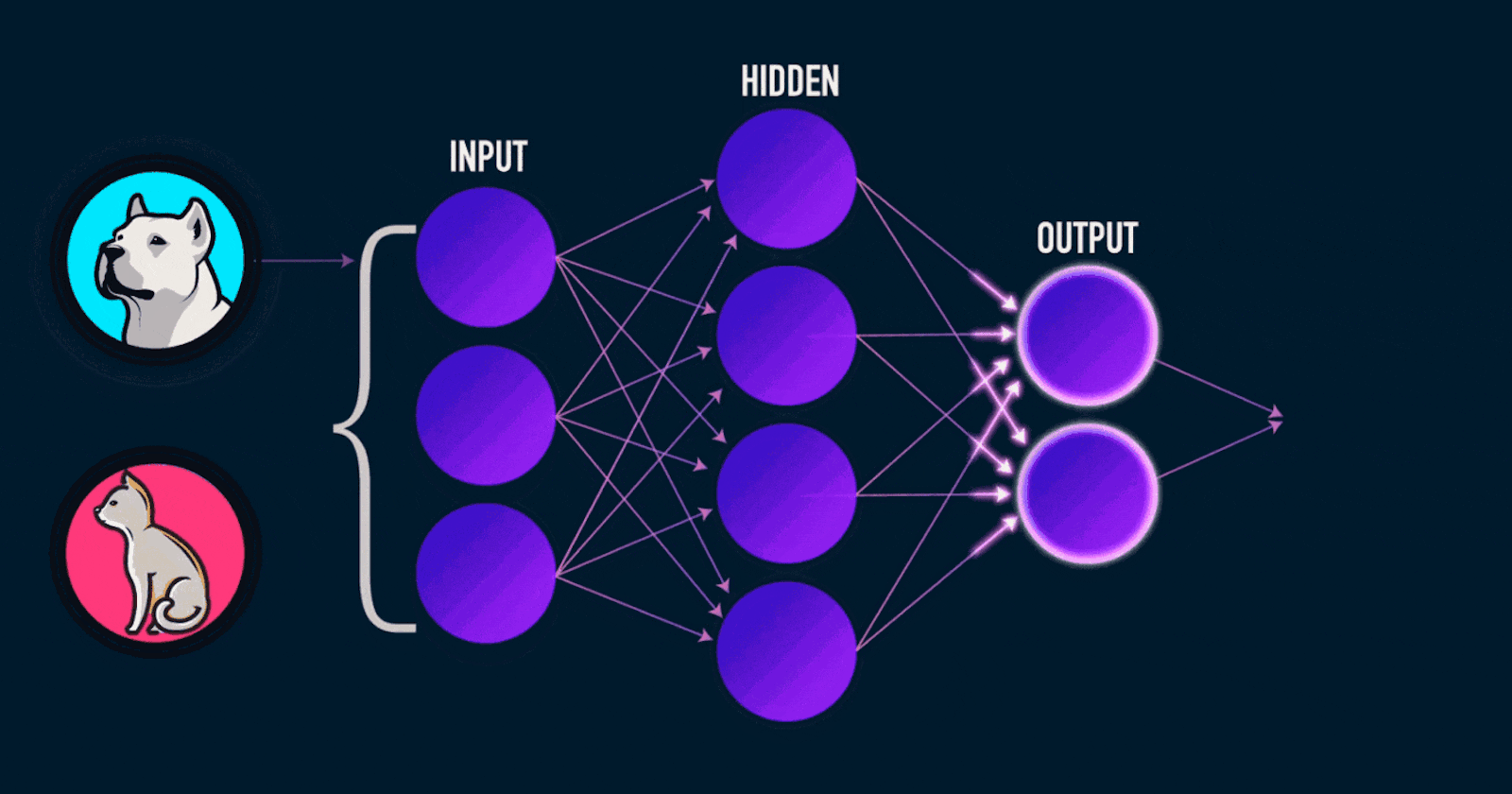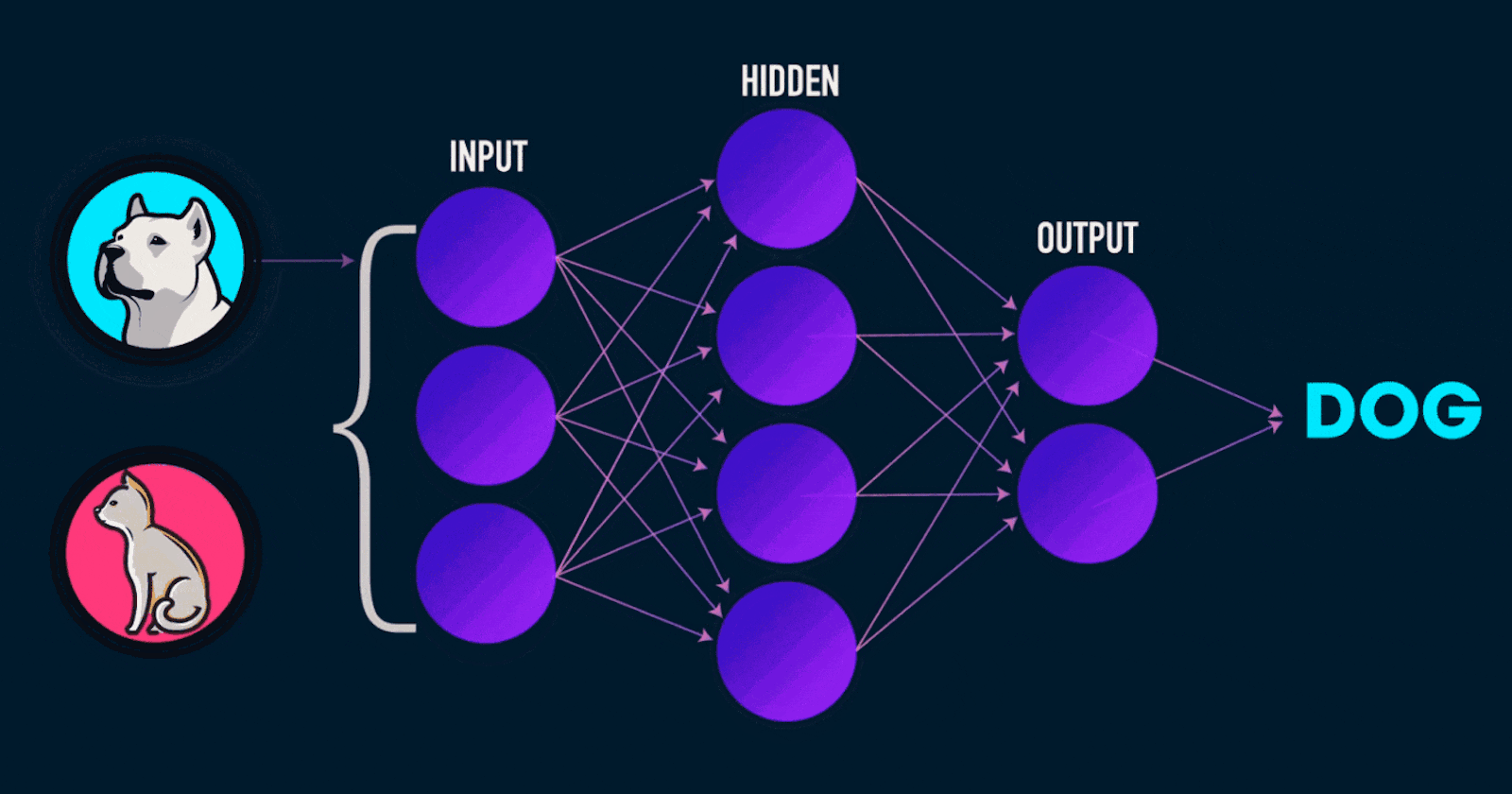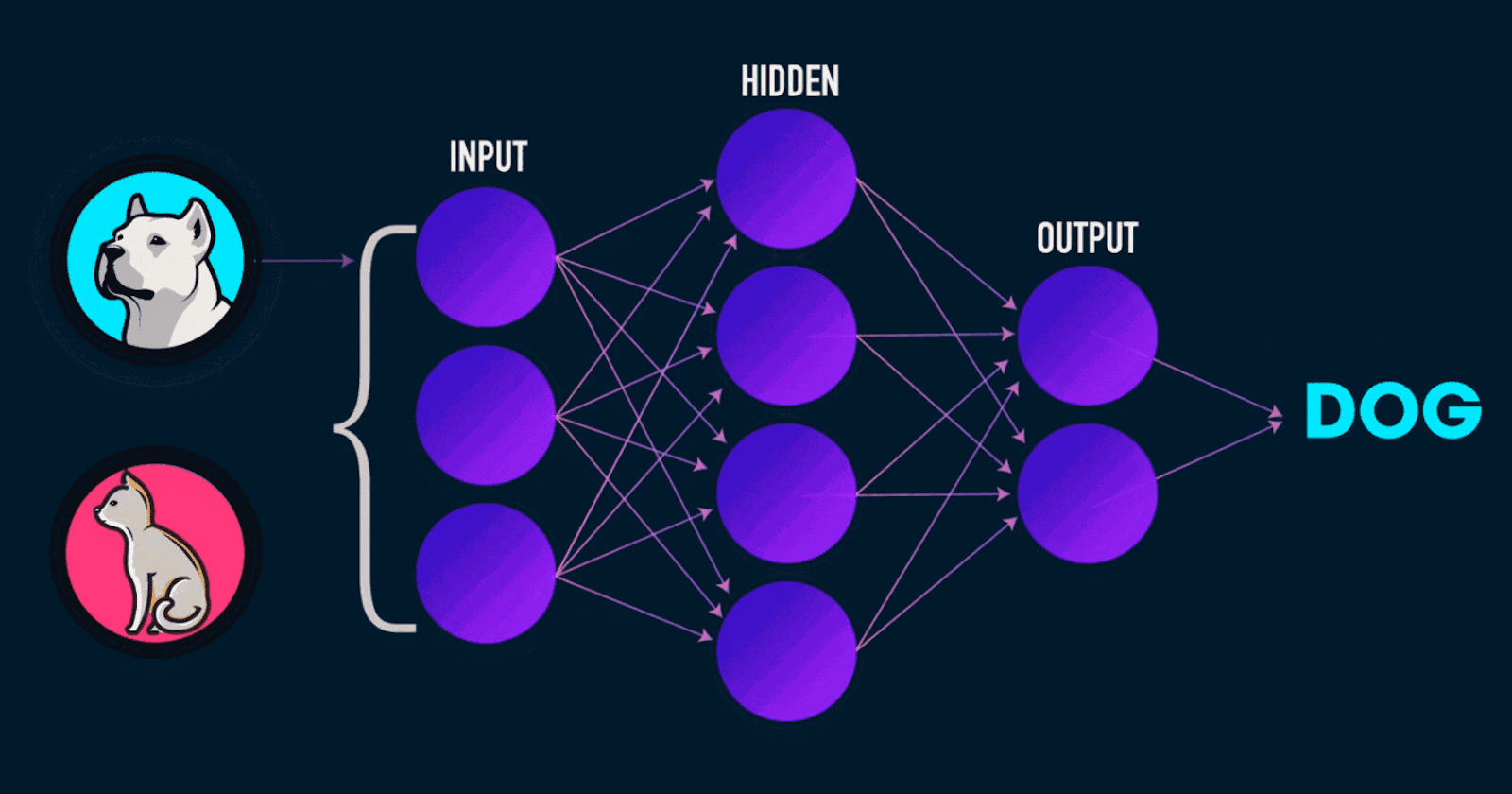
Given a dataset containing input features and true labels, the neural network learns the best-fit function to separate between different classes.
To learn the function, a three-step process is followed:
Forward propagation
Backward propagation
Update parameters
Forward Propagation
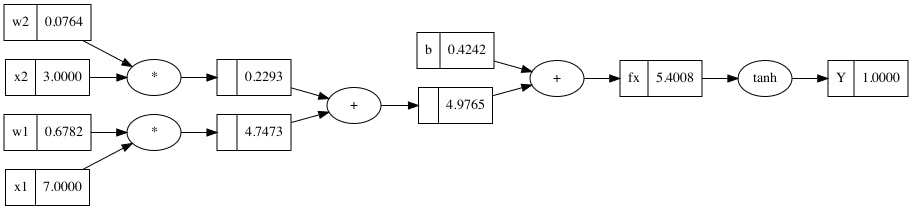
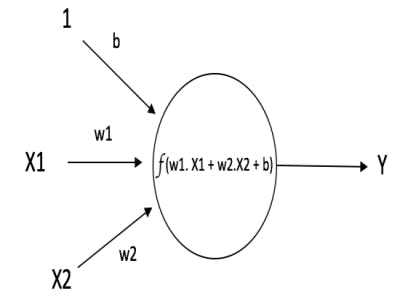
Suppose, we have two features (x1 and x2) in our dataset, then the output, f(x) is as follows:
$$f(x) = x_1 + x_2$$
For each input, we add weights and biases. Weights learn the effectiveness of each input and bias allows you to move the output function along the axis giving more control. Therefore, the linear equation for one neuron stands as follows.
$$f(x) = w_1x_1 + w_2x_2 + b$$
Let's create a Value class for forward propagation with vanilla python which is capable of arithmetic operations like multiplication and addition required in the forward pass.
class Value:
def __init__(self, data):
self.data = data
def __repr__(self):
return f'Value(data = {self.data:.4f})'
def __add__(self, other):
# if other is not an instance of Value then we cast it to Value
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data)
return out
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data)
return out
# Let c = 5 + b, this calls __radd__ method of b with 5 as argument
def __radd__(self, other):
return self + other
# Let c = 5 * b, this calls __rmul__ method of b with 5 as argument
def __rmul__(self, other):
return self * other
Now, let's initialize x1 = 7.0, x2 = 3.0 and set w1,w2 and b to some random values.
import random
x1, x2 = Value(7.0), Value(3.0)
w1, w2, b = (random.uniform(0, 1) for _ in range(3)) # a generator expression to create a tuple containing three random variable and unpacking them
fx = x1*w1 + x2*w2 + b # Here, fx is a Value object
print(fx)
This represents a linear forward propagation through one neuron.
Now, let's add non-linearity to learn more complex prediction functions, some common non-linear activation functions are -TanH, Sigmoid, and ReLU.
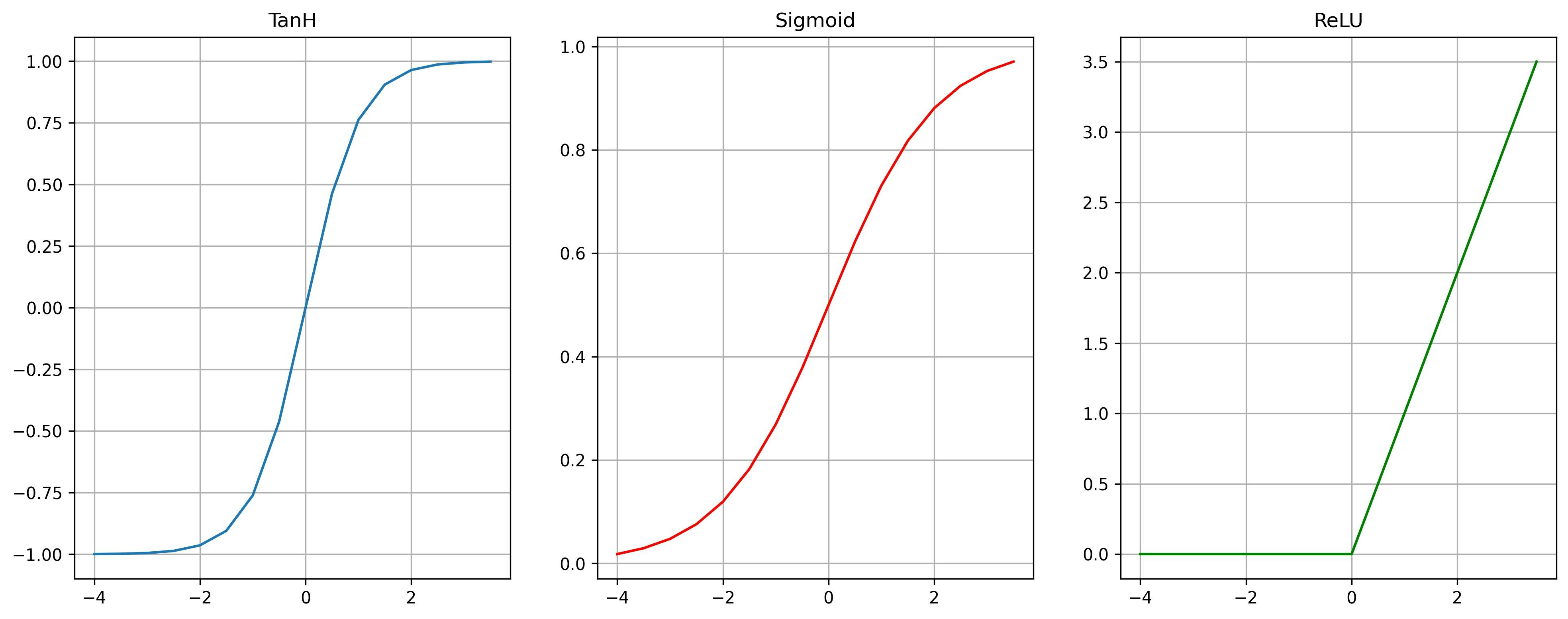
We will use TanH because it is a smooth function that has a range symmetric around zero, it helps to centre data reducing the effect of vanishing gradient.
import math
class Value:
# existing methods and attributes
def tanh(self):
x = self.data
out = Value((math.exp(2*x) + 1)/(math.exp(2*x) - 1))
return out
The output, Y after adding TanH is:
$$Y = tanh(fx)$$
fx = x1*w1 + x2*w2 + b
Y = fx.tanh()
Finally, the forward pass to calculate the final output, Y is complete and below is the computational graph representing the forward pass through one neuron.
Likewise, we pass the same input through a set of neurons, and then the output of those neurons is passed as input into another layer of neurons creating a multi-layer perceptron.
Special thanks to Andrej Karpathy for his outstanding content on youtube. I learned from his youtube channel and I am still learning. He has been a great teacher of Deep Learning and I love how teaches. :)